Zusammenhangsmaß für zwei Variablen mit unterschiedlichen Skalenniveaus

Für die Untersuchung von Zusammenhängen mit verschiedenen Skalenniveaus gilt, dass jeweils das Maß für die Variable mit dem niedrigeren Skalenniveau einsetzbar ist.
NACHTEIL: Dies führt zu einem Informationsverlust, da Informationen aus der Skala mit dem höheren Skalenniveau (Rangfolge der Merkmalsklassen, Größe der Merkmalswerte) nicht einfließen.

Eta berücksichtigt die Unterscheidung zwischen abhängiger und unabhängiger Variable. Dieser Koeffizient basiert auf der Berechnung des PRE-Maßes eta²  und beschreibt den Zusammenhang zwischen einer nominal- oder ordinalskalierten unabhängigen Variablen und einer intervallskalierten abhängigen Variable. Das Konzept eines PRE-Maßes soll hier nicht Gegenstand sein und wird daher nicht näher ausgeführt.
Grundsätzlich wäre Eta auch als Zusammenhangsmaß für zwei intervallskalierte Variablen einsetzbar, hierfür sind allerdings die speziellen Maße (siehe Korrelationskoeffizient) besser geeignet.

Berechnung des Zusammenhangsmaßes eta

Eta² berechnet sich folgendermaßen:
Die nominalskalierte Variable wird als unabhängige Variable (UV), die intervallskalierte Variable als abhängige Variable (AV) aufgefasst.
Beispiel: es wird ein Zusammenhang vermutet zwischen der Tageszeitung, die man liest (unabhängige Variable, nominalskaliert) und dem Bruttoeinkommen pro Monat (abhängige Variable, metrisch skaliert)
Der Einfachheit halber wird nur zwischen den Lesern regionaler Tageszeitungen (RZ) und den Lesern überregionaler Tageszeitungen (ÜZ) unterschieden.
Es liegen folgende Rohdaten vor: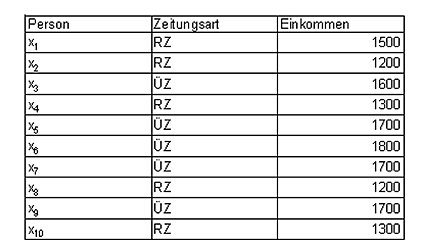

Gesamtmittelwert über alle Teilnehmer:

Prognose der Werte der AV, ohne die Werte der UV zu berücksichtigen.
Der beste Prognosewert für die Werteverteilung einer metrischen Variable (AV) ist das arithmetische Mittel, da hier per Definition die Summe der Abweichungsquadrate (= Prognosefehler) minimal ist, es ergibt sich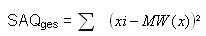

SAQges ist ein Maß für den Gesamtfehler, der sich ergibt, wenn die Werte der AV allein durch den Mittelwert der AV vorhergesagt werden.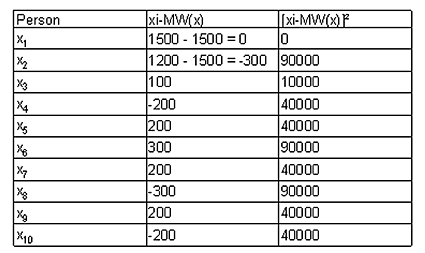

Es ergibt sich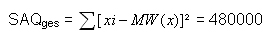

Prognose der Werte der AV unter Berücksichtigung der Werte der UV.
Es lesen 5 Personen Regionale Tageszeitungen (RZ) und 5 Personen Überregionale Tageszeitungen (ÜZ). Dabei ergeben sich folgende Mittelwerte:

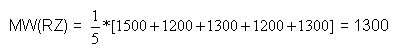
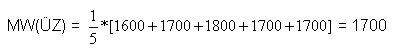
Es ergeben sich folgende spezifische SAQ-Werte für die Zeitungsart: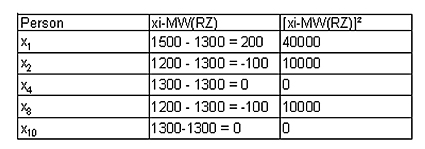

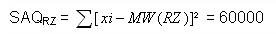
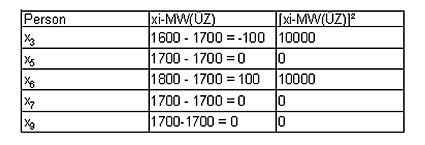
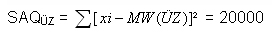
Die Summe der SAQ pro UV-Ausprägung ist ein Maß für den Gesamtfehler, der sich ergibt, wenn die Werte der AV auf der Basis der Werte der UV prognostiziert werden: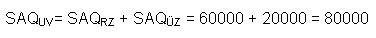

Berechnung von Eta²:
auf der Basis der Prognoseverbesserung von Schritt 2 nach Schritt 3 kann der Zusammenhang zwischen den beiden Variablen bestimmt werden.
Es gilt: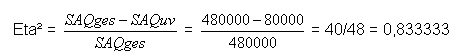

Berechnung von Eta
Um daraus das Zusammenhangsmaß eta zu erhalten, muss die Wurzel gezogen werden: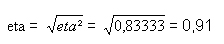

Berechnung von eta mit Hilfe von SPSS

Wandeln Sie Ihre nominale Variable für die SPSS-Berechnung in Zahlenwerte (z.B. RZ = 0, ÜZ = 1) um.
Wählen Sie im Menü „Analysieren“ --> „Deskriptive Statistiken“ --> „Kreuztabellen“.
Es öffnet sich folgendes Fenster:

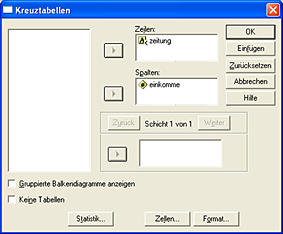
WICHTIG: Ordnen Sie das nominalskalierte Merkmal (hier: Zeitung) in die Zeilen, das intervallskalierte (hier: Einkommen) in die Spalten ein. Klicken Sie dann auf den „Statistik“-Button. Es öffnet sich folgendes Fenster:

Wählen Sie unter „Nominal bezüglich Intervall“ die Option „Eta“ aus. Klicken Sie auf den „Weiter“-Button.
Ergebnisse für Eta werden in SPSS folgendermaßen ausgewiesen:

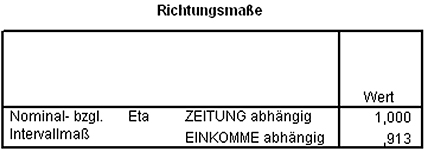
SPSS zeigt immer zwei Zusammenhänge an (siehe oben). Die Werte beziehen sich dabei immer auf die nominalskalierte Variable.

Die Ergebnisanzeige ist folgendermaßen zu lesen:
Der Eta-Wert in der ersten Zeile ist immer 1. Es handelt sich um den Zusammenhang der nominalskalierten Variable (hier: ZEITUNG) mit sich selbst.
Die für die Interpretation wichtige Maßzahl ist der zweite Wert der Ergebnisausgabe. Dieser stellt den Zusammenhang zwischen nominalskalierter (hier: Zeitung) und intervallskalierter Variable (hier: EINKOMMEN) dar.
SPSS bestätigt unseren manuell berechneten Wert von Eta = 0,91.

Interpretation
Der Wertebereich für Eta liegt zwischen 0 und 1. Ein Wert größer 0,3 kann bereits als recht starker Zusammenhang betrachtet werden.
Der Eta-Koeffizient zeigt allerdings nicht die Richtung des Zusammenhangs an (verdienen RZ- oder ÜZ-Leser monatlich mehr Geld?). Um Aussagen über die Richtung des Zusammenhangs treffen zu können sind weitere statistische Vorgehen notwendig.

Man kann für unser Beispiel also die Schlussfolgerung ziehen, dass es einen sehr starken Zusammenhang gibt zwischen der Art der Zeitung, die man liest und dem eigenen Einkommen.

Ein kausaler Schluss ist jedoch nicht möglich: Man kann keine Aussage darüber treffen, ob Personen mehr verdienen, weil sie eine bestimmte Zeitungsart lesen oder ob sie überregionale Zeitungen lesen, weil sie mehr verdienen.